A brief history of triangles

thanks, Pythagoras

Before I begin, I ought to apologise for not posting for almost a month. From now on, I will be uploading regularly (fortnightly). Thanks for all your patience.

Alright, enough with the melancholy tone… this post is meant to be a bit of fun; you know, geometry - what could be more enjoyable?

First and foremost, I shall assume that you are all fully aware of what a triangle is (although mathematicians don’t like assumptions; that shall soon be made blatantly obvious). If you’re still unsure, there’s a bit of a hint below:

image credit: Tusik Only / Unsplash

Moving on, as the title suggests, I’ll be doing a bit of a Stephen Hawking and discussing, yes, a brief history of time these mysterious three-sided shapes.

So, let’s start with a simple theorem that (hopefully) everyone’s aware of:

\(a^2 + b^2 = c^2\)

And hopefully, you all know its name (the Pythagorean theorem). It applies to - and you wouldn’t believe it - triangles! Particularly the ones that have one of these:

image credit: analyzemath.com

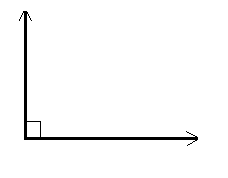
That's right: a totally normal right angle. Basically, you label one side ‘a’, another side ‘b’, and the hypotenuse (the long one) ‘c’. Then the above equation applies. And that equation is called the Pythagorean theorem because, well, you’d never guess; it was (allegedly) created by an ancient Greek dude named Pythagoras (of Samos [below]), who incidentally led a religious cult that believed in the philosophy of Pythagoreanism.

image credit: Encyclopædia Britannica

But was the theorem that was named after him actually created by him? Just as you’d expect, the answer is, well… we don’t really know, but probably not because there’s a good old bit of evidence that people actually knew of it before this stereotypically smart old wise philosopher guy was even born. Indeed, the ancient Egyptians knew of the 3-4-5 triangle (a good, old Pythagorean triple; don’t worry, we’ll get onto that stuff), and they basically used that fact to make perfect corners when they were constructing things - namely, the pyramids and all that jazz. And then there’s the Babylonians because there’s always the Babylonians, and they like numbers and stuff. So a collection of their numbers was found on a tablet that someone decided to call Plimpton 322, dating back to c1800 BCE (for reference, Pythagoras was alive around 570-490~ish BCE) that included intriguing pairs of (some very, very large) numbers of trigonometric (triangle-y) curiosity.

---

A brief note on Pythagorean Triples

Before I explain further the significance of Plimpton 322 [P322], I should probably endeavour to define a little rule of three (no, not a tricolon, for you English students). This so-called rule of three is what is known as a Pythagorean triple. In essence, such a triple is a group of three positive integers (a, b and c) such that a right-angled triangle exists with side lengths a, b and c (with c being the hypotenuse), thus satisfying the equation stated previously. For example:

\(3^2 + 4^2 = 9 + 16 = 25 = 5^2\)

So 3-4-5 is a Pythagorean triple. We can also call it a primitive Pythagorean triple because 3, 4, and 5 are relatively prime (don’t share a common factor - they obviously fell out). Triples like 6-8-10, for example, are not primitive as they are all BFFs and share a common factor (2, in this case). Pythagoras and the Babylonians came up with a general formula for generating (not exclusively primitive) triples:

\((2m, m^2-1, m^2+1)\)

corresponding to (a, b, c), where m is a positive integer > 1.

A very unnecessary interjection:

In 1643, Fermat challenged Mersenne to find a Pythagorean triple whose hypotenuse and sum of the other sides were square numbers (because why not?). Fermat found the smallest possible solution:

\(a = 4565486027761, b = 1061652293520, c = 4687298610289\)

where

\(c = 2165017^2, a + b = 2372159^2\)

¹ Funky stuff. Anyway…

Back to the future Babylonians

So, the Babylonians seem to have known about Pythagorean triples before they were actually called Pythagorean triples and decided to make a little tablet out of it (pictured below)…

Plimpton 322 (image credit: Columbia University)

in plain English (image credit: Columbia University)

We have in the above table

\(w^2 + l^2 = d^2\)

where corrections are in red. Nobody knows why the tablet was constructed. Perhaps it was an early form of trigonometry, or maybe it was an arithmetic aid. Either way, it’s advanced - very advanced - for c1800 BCE. And also kinda cool (you can thank me later).²

---

A proof and a problem

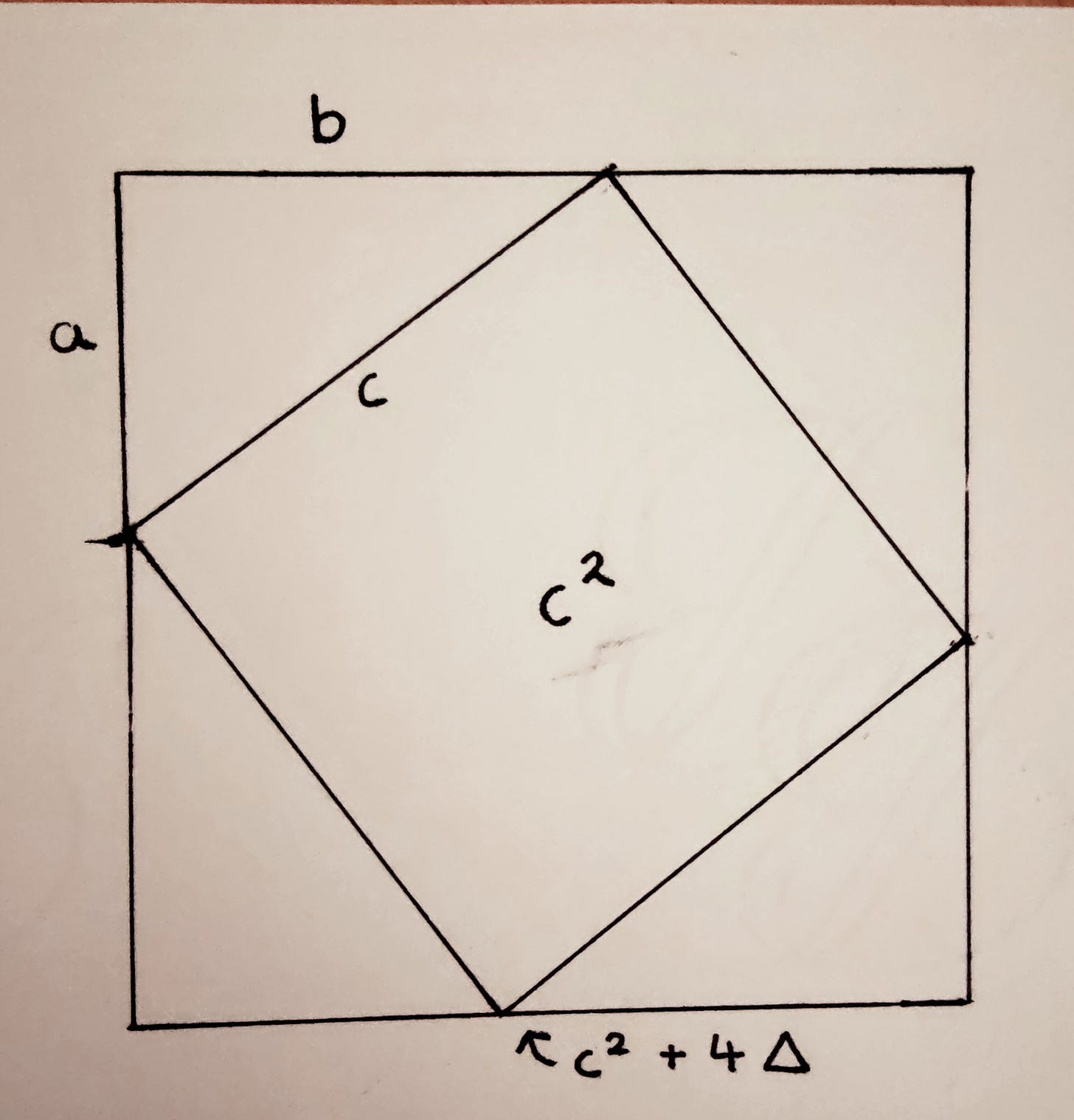
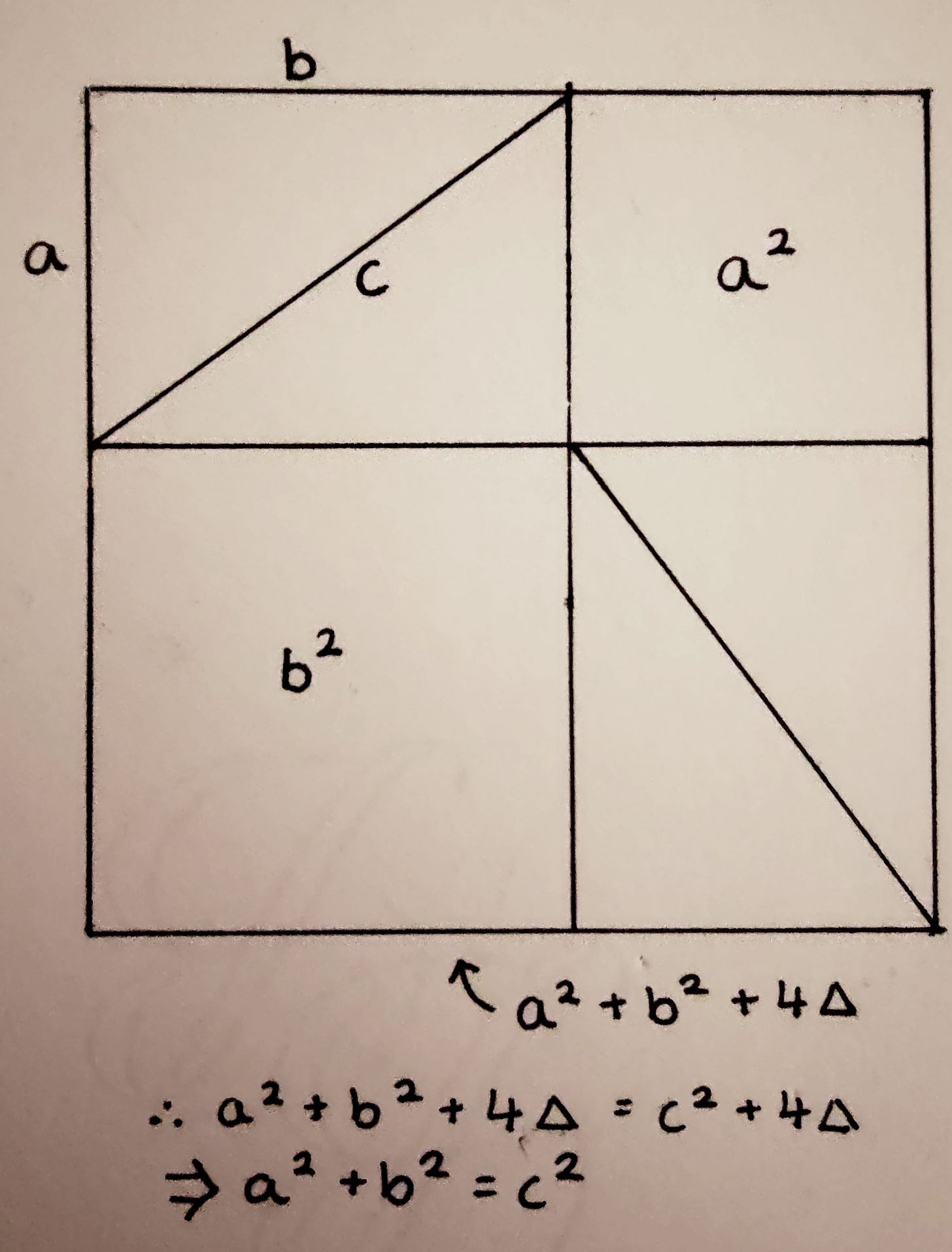
Finally, I thought I’d give you one (of the many) proofs of the Pythagorean theorem (drawn by moi) and a neat problem to wrap this post up rather nicely…

The proof

It’s not necessarily the height of mathematical rigour, but I think it’s a rather charming geometric proof (for reference, hundreds exist - you can buy yourself a book of them if you wish…)

part 1…

…and part 2

[N.B. I did not create this proof - I happen to remember it from a lecture.] Anyway, I hope it’s all clear enough.

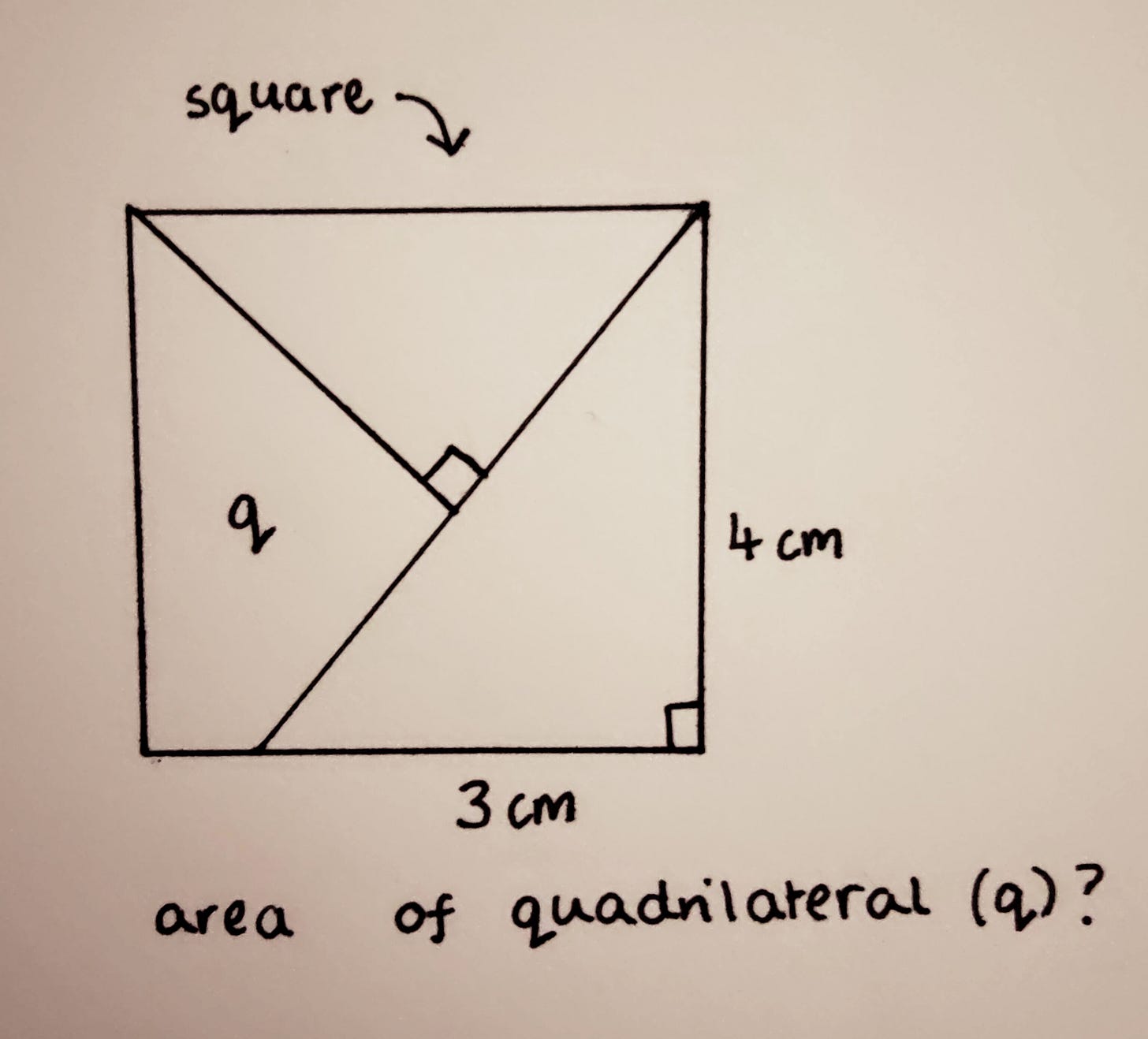
And to finish, a neat problem as promised:

My rather hopeless drawing attempts to convey two right-angled triangles and an irregular quadrilateral (q) within a square. Ideally, you remember a bit about Pythagorean triples, how to find the area of a square, as well as alternate angles and similar triangles (which I obviously haven’t covered today, but I have provided links for). I will post the worked solution in the comments next Sunday, but feel free to post your answers (to 3 s.f.) in the comments below anytime before then - I look forward to seeing them!

---

Okay… that’s all for today. As always, don’t forget to brutally destroy the buttons below. Enjoy the rest of your day!

1. Weisstein, Eric W. “Pythagorean Triple.” MathWorld--A Wolfram Web Resource. Available at: https://mathworld.wolfram.com/PythagoreanTriple.html (Accessed: 29 October 2023).

2. Casselman, B. (2003) “The Babylonian tablet Plimpton 322.” UBC Math. Available at: https://personal.math.ubc.ca/~cass/courses/m446-03/pl322/pl322.html (Accessed: 29 October 2023).